Heapsort

Baum und Heap

Def.:

Ein binärer Baum ist entweder leer oder besteht aus einem Knoten, dem zwei binäre Bäume zugeordnet sind. Dieser heißt dann Vater des linken bzw. rechten Teilbaums. Ein Knoten ohne Vater heißt Wurzel. Die Knoten, die $x$ zum Vater haben, sind seine Söhne. Knoten ohne Söhne heißen Blätter.

Ebene $0=$ Wurzel. Ebene $i+1=$ Söhne von Ebene $i$.

Def.:

Ein Heap ist ein binärer Baum mit $n+1$ Ebenen, in dem die Ebenen $0,1,\ldots , n-1$ vollständig besetzt sind; Ebene $n$ ist von links beginnend bis zum so genannten letzten Knoten vollständig besetzt. Die Knoten enthalten Schlüssel. Der Schlüssel eines Knotens ist kleiner oder gleich den Schlüsseln seiner Söhne.

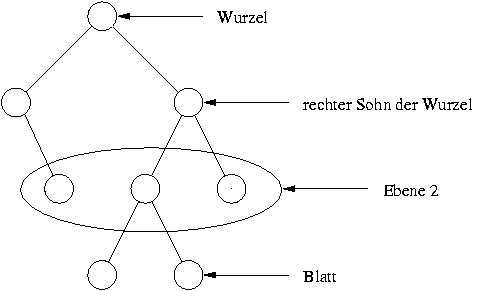
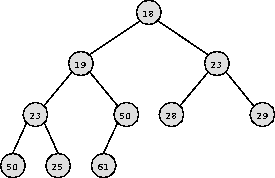
Offenbar steht der kleinste Schlüssel eines Heaps in der Wurzel.

Idee für Heapsort:

Verwendet wird ein Heap als Datenstruktur, die das Entfernen des Minimums unterstützt.

Gegeben seien die Schlüssel $a_{1},\ldots ,a_{n}$.

Baue einen Heap auf mit den Schlüsseln $a_{1},\ldots ,a_{n}$.
do {
     entferne Wurzel; // = Minimum
     reorganisiere Heap;
} while (Heap ist nicht leer);

Idee für Wurzelentfernen:

Entferne ``letzten'' Knoten im Heap und schreibe seinen Schlüssel in die Wurzel.
Vertausche so lange Knoten mit ``kleinerem'' Sohn, bis Heapbeziehung eintritt.

Idee für Implementation: Die Knoten werden wie folgt nummeriert:
Wurzel erhält Nr. $0$,
linker Sohn von Knoten $i$ erhält die Nr. $(2\cdot i + 1)$
rechter Sohn von Knoten $i$ erhält die Nr. $(2\cdot i+2)$

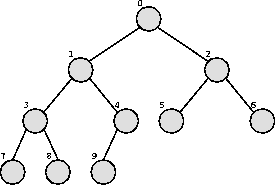
Im Array

double[] a = new double [n];

steht in a[i] der Schlüssel von Knoten $i$.

Vorteil:

Die Vater/Sohn-Beziehung ist allein aus dem Knotenindex zu berechnen.
$2i+1$ bzw. $2i+2$ heißen die Söhne von $i$
$(i-1)/2$ heißt der Vater von $i$.

Source: HeapSort.java     JavaDoc: HeapSort.html    

Aufwand für die Konstruktion eines Heaps

Sei $h$ die Höhe eines Heaps. Sei $n - 1=2^{h}-1$ die Anzahl der Elemente, z.B. $15=2^ {4}-1$.

Ebene	Sickertiefe	Anzahl
$h-1$	$1$	$\frac{n}{2}$
$h-2$	$2$	$\frac{n}{4}$
$h-3$	$3$	$\frac{n}{8}$
$\vdots$	$\vdots$	$\vdots$
$0$	$h$	${\displaystyle \frac{n}{2^{h}}=1}$

Anzahl der Schritte:

$$\begin{eqnarray*} \sum_{i=1}^{h}c\cdot i\cdot \frac{n}{2^i}=c \cdot n\cdot \sum_{i=1}^{h}\frac{i}{2^{i}} \end{eqnarray*}$$

$\Rightarrow$ Aufwand $O(n)$, denn: $\frac{1}{2}+\frac{2}{4} +\frac{3}{8}+\ldots < 2$

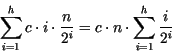
Aufwand für einmaliges Minimumentfernen: $O( \log n)$

$\Rightarrow$ Gesamtaufwand: $O(n)+O(n\cdot \log n)=O(n\cdot \log n)$

     für best, average und worst case.

Weitere Einsatzmöglichkeit des Heaps

Verwende eine dynamisch sich ändernde Menge von Schlüsseln mit den Operationen

$\bullet$	initheap	legt leeren Heap an
$\bullet$	get_min	liefert das momentan Kleinste
$\bullet$	del_min	entfernt das momentan Kleinste
$\bullet$	insert(x)	fügt $x$ hinzu
$\bullet$	heapempty	testet, ob Heap leer ist

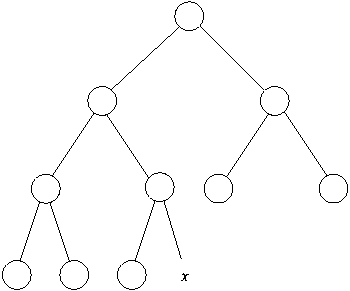
Idee für Einfügen: (schlecht: von oben nach unten)
besser: Füge neues Blatt mit Schlüssel $x$ an, und lasse $x$ hochsickern.

i = neuer Index;
while (a[i] < a[vater(i)]){ 
   tausche a[i] mit a[vater(i)];
   i = vater(i);
}

Aufwand $O( \log n)$