Tesselation
Vortrag im Rahmen des Seminars Computergrafik
II
Leiter: Dipl.-Phys. Olaf Müller
Student: Amir Sekic
Tesselation
Tesselation ist eine
Technik, die sich mit der Zerlegung von Polygonen beschäftigt. Dabei spielen
die Genauigkeit, die Schnelligkeit und die Einfachheit eine große Rolle, wie
auch bei den meisten anderen, Polygone bearbeitenden, Techniken wie Consolidation
und Simplification.
Die Polygone werden bei der Tesselierung
in so genannte primitive Flächen, wie z.B. Dreiecke oder Vierecke zerlegt, da
solche Flächen leichter zu handhaben sind als komplexe Polygone (insbesondere
konkave).
Die Dreieckszerlegung der Polygone nennt man auch Triangulation.
Das englische Wort to tesselate kommt ursprünglich aus dem lateinischen und bedeutet mit Mosaik pflastern, mit einem Muster überziehen.
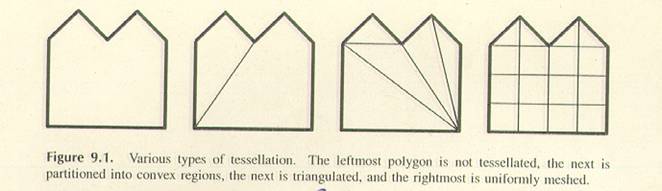
Es gibt
verschiedene Typen von Tesselation, die man in folgendem
Bild sehen kann.
Wieso
tesseliert man?
Die meisten heutigen Grafik-APIs und Grafikkarten sind optimiert für Dreiecke. Da Dreiecke planar und konvex sind wird das Scanline-Verfahren nur auf Dreiecke angewandt, was zur Vereinfachung und Beschleunigung des Renderings führt. Wenn man auf die komplexeren Polygone das Scanline-Verfahren anwenden will, ist der Aufwand etwas großer, wobei die Hohlräume und Kantenüberschneidungen zusätzlich eine Rolle spielen.
Manche APIs arbeiten auch auf konvexen Polygonen, was keine große
Rolle spielt, da der Aufwand um ein konvexes Polygon in Dreiecke zu zerlegen
sehr klein ist. Ein konvexes Polygon lässt sich triangulisieren,
indem man von einem beliebigen Eckpunkt aus zu allen nicht benachbarten
Eckpunkten Diagonalen zieht.
Wenn man bei einer
Fläche Schatten und Beleuchtung besser regulieren will, kann man ein Netz über
die Fläche ziehen, was zur einer besseren Bildqualität
führt.
Tesselation ist nur dann
sinnvoll, wenn man kleine Teile der Fläche separieren will, um diese getrennt
zu bearbeiten.
Um eine Tesselierung durchzuführen, entwickelt man sogenannte Tesselators, worauf im ersten Kapitel weiter eingegangen
wird.
In den anderen
Kapiteln wird auf einzelne Probleme näher eingegangen; sowohl auf solche, die
gelegentlich beim korrekten Tesselieren auftreten, wie
auch derartige, die beim falschen Tesselieren
entstehen können.
1.0 Tesselators
Unter dem
Oberbegriff Tesselators verbergen sich alle voneinander verschiedenen
Implementierungen zur Tesselation. Einen robusten und vor allem generellen
Tesselator zu implementieren ist sehr schwierig. Beim Tesselieren
können zwei Probleme auftreten, welche man manchmal nicht so leicht vermeiden kann.
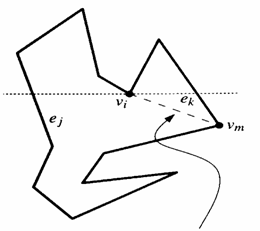
Das erste Problem
entsteht beim Projezieren, wenn sich zwei Kanten bei einem
Viereck überschneiden.
Das zweite entsteht
wenn ein Polygon mehrere äußere und nur eine innere Region hat, wenn also ein Polygon
Hohlräume besitzt.
Nach dem Testen auf
diese zwei Probleme kommt man zur eigentlichen Aufgabe, der Dreieckszerlegung.
Eine Methode wird im Kapitel Polygon Triangulation vorgestellt.
1.1
Kantenüberschneidungen
( self-intersection )
Das Erste, was ein
Tesselator tun soll, ist herauszufinden, wie man ein 3-D Polygon am besten in
2-D projezieren kann.
Damit werden das
Problem der Zerlegung in simple Polygone und der zugehörige Algorithmus
vereinfacht.
Eine Methode ist
eine der x, y, z Koordinaten zu löschen, das heißt das Polygon wird in eine der
xy, xz, oder yz Ebenen projeziert.
Meistens ist die
Projektionsseite mit der größten Projektionsfläche die beste (man benutzt die
gleiche Technik wie für den Punkt im Polygon Test). Dabei ist
die Gefahr einer self-intersection viel kleiner.
Die Fläche kann
direkt berechnet werden oder man setzt die Koordinate der Normale mit dem
größten Betrag auf Null.
Betrachtet man zum
Beispiel eine Normale mit den Koordinaten (-6, 2, 4), so nimmt man die
x-Koordinate (–6), den sie hat den größten Betrag.
Dieses Verfahren
eliminieren die meisten, aber nicht alle Kantenüberschneidungen.
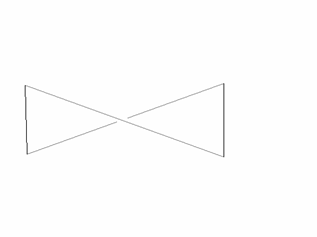
Bei
Kantenüberschneidungen entsteht ein sogenanntes Bowtie
–Viereck (siehe Bild unten).
Von der
theoretischen Seite her kann man folgendermaßen überprüfen, ob
Kantenüberschneidungen vorliegen:
Seien f1(s) = r1 + s*d1
und f2(t) = r2 +
t*d2 zwei parametrisierte
Gradengleichungen .
Wenn man setzt :
1: f1(s) = f2(t)
2: r1
+ s∙d1 = r2 + t∙d2
Multipliziert man
einmal mit dem Vektor d2 ^ , der orthogonal
zu d2 ist, und einmal mit dem Vektor d1 ^ , der orthogonal
zu d1 ist, erhält man folgendes:
3: s∙d1 * d2 ^ = ( r1 - r2 ) * d2 ^ da
d1 * d1 ^ = 0 und d2 * d2 ^ = 0
t∙d2 * d1 ^ = ( r1 - r2 ) * d1 ^
“ *
” -
bezeichnet den Skalarprodukt
4: s
= ( r2 - r1 ) * d2 ^ / ( d1 * d2 ^ )
t = ( r1 - r2
) *
d1 ^ / ( d2 * d1 ^ )
Wenn d1 * d2 ^ = 0
(dann ist d2 * d1 ^ auch Null) also d1
und d2 parallel sind, dann sind die Geraden auch parallel. Das heißt,
wenn s und t endlich groß sind, schneiden sich die Geraden.
Für endlich lange Strecken
der Länge l1 und l2 die in
p1 und q1 (s = t = 0) starten und in p2
und q2
(s = l1 , t = l2
) enden, erhält man folgendes:
r1 =p1,
d1 = p2 – p1,
r2 =q1, d2
= q2 – q1 t = (r1
- r2 ) * d1 ^ / (d2 * d1 ^ ) .
Wenn t und s aus [0,1] sind, dann schneiden sich
die beiden Linien f1(s) und f2(t),
sonst nicht.
Von der praktischen
Seite aus gesehen, stellt sich diese Tatsache dann folgendermaßen dar:
Wir verwenden die
gleiche Notation wie oben:
Seien f1(s) = p1 + s∙( p2 - p1
) und f2(t) = q1 +
t∙( q2 - q1
) die zwei Linien (Polygonkanten)
Wenn man das
gleiche Verfahren wie oben für f1(s) = f2(t) benutzt,
erhält man Folgendes:
s = ( - c * a^ ) / ( b * a^ ) = ( c * a^ ) / ( a * b^ ) = d / f
t = ( c * b^ ) / ( a * b^ ) = e / f
Wobei a = q2 – q1, b = p2 – p1,
c = p1 – q1, d = c * a^, e = c * b^ und f = a * b^ ,
a^ und b^ sind
Vektoren die orthogonal zu a und b sind.
Das Vereinfachen
des Faktors s geschieht mit Hilfe von a^ * b = - b^ * a und a * b^ = b^ * a
.
Wenn a * b^ = 0, sind die Linien kollinear.
Solange man s und t
nicht explizit braucht, kann man folgenden Code benutzen, um zu testen,
ob 0 £ s £ 1 :
if ( f > 0 )
If (d < 0 or d > f
) return NO_INTERSECTION;
else
if (d > 0 or
d < f ) return NO_INTERSECTION;
Bei diesem Test
wird die Division vermieden, was zur Verbesserung der Effizienz führt.
Nach diesem Test
ist sichergestellt, dass 0 £ s £ 1
.
Entsprechendes
prüft man für t = e / f (d tauscht man durch e aus). Wenn der Test
kein NO_INTERSECION liefert, bedeutet das, dass sich die Linien schneiden.
In dem Fall
versucht man das Polygon in eine andere Projektionsebene zu projezieren.
1.3 Hohlräume
Die Idee, Hohlräume
zu beseitigen ist folgende: Man verbindet zwei Vertizes,
welche sich auf verschiedenen Kanten befinden, wobei die Kanten verschiedene
äußere Regionen haben.
Dabei soll ein
einfaches Polygon entstehen. Man erhält dann ein Polygon mit nur noch einer
inneren und einer äußeren Region.
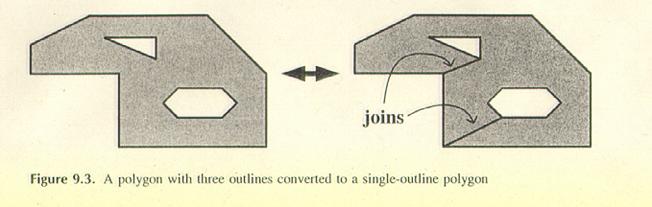
Bei Hohlräumen ist außerdem
die (winding number) Umlaufzahl zu beachten.
Die Umlaufzahl gibt
an, wie oft der Punkt von der Kontur des Polygons umlaufen wird, bzw. wie viele
Konturen ihn umschließen.
Ein Umlauf gegen
den Uhrzeigersinn wird (für einen Bereich und alle weiteren inneren Bereiche)
positiv angerechnet, ein Umlauf im Uhrzeigersinn negativ.
Hierbei geht man
von Außen nach Innen vor. Für jeden Punkt in einem Bereich ist die Umlaufzahl
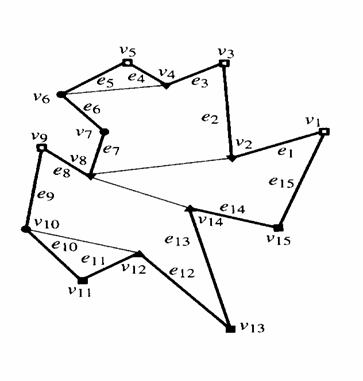
natürlich gleich. Das Bild zeigt Beispiele für Polygone mit Regionen und deren Umlaufzahl.
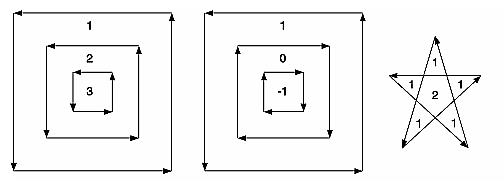
Die Umlaufregel
klassifiziert einen Bereich als Innen, wenn die Umlaufzahl zu einer bestimmten
gewählten Kategorie gehört. Unterschieden werden dabei folgende Kategorien: ungerade,
ungleich null , positiv, negativ und Betrag ³ 2.
Durch diese
Kategorien werden Teile des Polygons als Außen und andere Teile als Innen
definiert. Die Wahl der Kategorie bestimmt also wo Außen und wo Innen ist.
Meistens werden die
Kategorien „ungerade“ oder „ungleich null“ verwendet, um das Innere eines
Polygons zu bestimmen.
Das Bild zeigt für
alle Kategorien einige Beispiele, wie die Polygone bei dieser Wahl aufgeteilt
werden.
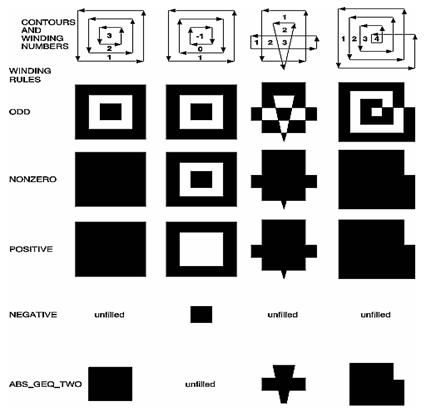
1.4 Polygon
Triangulation
In diesem Teil wird
die Dreieckszerlegung von Polygonen ohne Kantenüberschneidungen und Hohlräume
behandelt. Man geht hierbei davon aus, dass alle Kantenüberschneidungen und
Hohlräume durch die oben beschriebenen Verfahren beseitigt worden sind.
Der erste Schritt
in diesem Verfahren ist die Zerlegung in sogenannte monotone Regionen
(Polygone). Im zweiten Schritt werden dann die monotonen Teile in Dreiecke
zerlegt.
Definition:
Ein Polygon ist monoton in Beziehung zur Linie l wenn für jede Linie l| , die orthogonal
zur Linie l ist, beim Schneiden mit dem
Polygon eine Linie oder ein Punkt entsteht.
Definition:
Punkt p ist oberhalb von q, wenn py £ qy und px > qx ,und p ist unterhalb
von q, wenn py ³ qy und px
< qx .
Hierbei sind px und qx die
jeweiligen x-Werte von p und q, py und qx die jeweiligen y-Werte.
Wir können ein
Polygon folgendermaßen in monotone Regionen zerlegen:
Man beginnt beim Vertex mit dem größten y-Wert und folgt dann der
Polygonkante im Uhrzeigersinn. Ein Vertex, bei dem wir die Richtung von oben
nach unten oder von unten nach oben ändern, bezeichnen wir als Turn Vertex.
Es werden fünf
verschiedene Arten von Turn Vertizes definiert:
Einen Start-Vertex hat man, wenn die Nachbarn unterhalb liegen
und der innere Winkel ß < 180° ist .
Einen End-Vertex, wenn die Nachbarn oberhalb liegen und ß < 180°.
Einen Split-Vertex, wenn die Nachbarn unterhalb liegen und ß >
180°.
Einen Merge-Vertex, wenn die Nachbarn oberhalb liegen und ß > 180°.
Alle anderen
Vertices nennt man reguläre Vertizes.
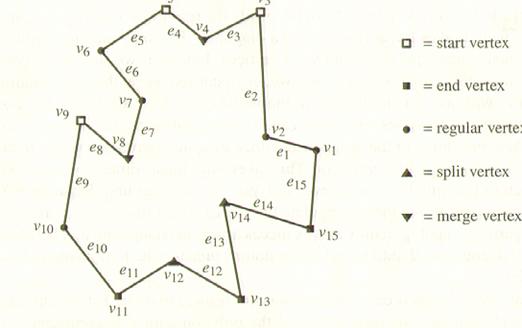
Im Falle py = qy
werden die Vertizes im Uhrzeigersinn abgelaufen
(der Vertex mit dem kleineren x - Wert kommt zuerst).
Um ein monotones
Polygon zu bekommen, müssen wir die Merge- und Split-Vertices beseitigen.
Dies geschieht
durch das Ziehen von Diagonalen zu anderen Vertizes
des entsprechenden Polygons.
Bei Split-Vertizes geht man folgendermaßen vor:
Eine imaginäre
Linie l wird solange von unten nach oben bewegt, bis sie auf einen Vertex trifft.
Wenn sich der Vertex oberhalb des Split-Vertex
befindet und die Verbindungslinie zwischen dem Split-Vertex
und dem Ziel-Vertex im Polygon liegt, dann entsteht
eine neue Kante und das Polygon wird geteilt.
Sonst wird die
Linie zum nächst oberhalb liegenden Vertex bewegt.
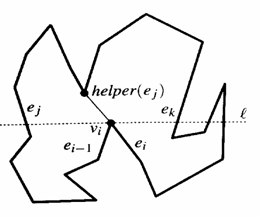
Im Falle eines Merge-Vertex wird die Linie l von oben nach unten bewegt. Der
erste unterhalb liegende Vertex, bei dem die
Verbindungslinie mit dem Merge-Vertex im Polygon
liegen würde, wird mit diesem verbunden.
Nach dem ersten Schritt bekommt man folgendes Bild.
Nun ist die Zerlegung in monotone Regionen abgeschlossen und wir
wenden uns der eigentlichen Dreieckszerlegung zu.
1.4.1 Dreieckszerlegung
monotoner Polygone
Sei P ein y - monotones Polygon mit n Vertizes. Die n Vertizes werden
nach ihren y-Werten sortiert.
Dann bewegt man sich
vom obersten Vertex zum untersten.
Wenn zwei Vertizes den gleichen y-Wert haben, so behandelt man den
mit dem kleineren x - Wert zuerst (Im Uhrzeigersinn).
Der Algorithmus
verarbeitet die sortierten Vertizes der Reihe nach,
beginnend mit dem Vertex mit dem grössten
y-Wert. Es wird ein Keller S angelegt, auf welchen diejenigen Vertizes gelegt werden, zu denen noch Diagonalen hinzugefügt
werden können. Wenn man einen Vertex bearbeitet,
zieht man so viele Diagonalen wie möglich zu den Vertizes,
die sich noch auf dem Keller befinden, wobei die Diagonalen im Polygon liegen
müssen. Vom letzten Vertex mit dem kleinsten y-Wert
aus wird versucht, Diagonalen zu allen anderen Vertizes
außer dem ersten und letzten zu ziehen.
Der Algorithmus hat
folgende Struktur:
Die sortierten Vertizes werden in einer doppeltverketteten Liste D
gelagert.
Seien u1 ,u2,
...,un
die sortierten Vertizes.
Man initialisiert
einen leeren Keller S und u1 ,u2,
...,un werden auf den Keller gepackt.
for j <= 3 to n - 1
do if
uj und der Vertex oben auf S auf verschiedenen Kanten liegen
then
alle Vertizes werden von S gepopt, Setzen einer Diagonale in D von uj
zu jedem gepopten Vertex
außer dem letzten.
uj - 1 und uj werden auf S gepusht.
else
ein
Vertex wird von S gepopt. Die anderen Vertizes aus S werden gepopt,
solange die Diagonalen in D sind.
Der
letzte Vertex der gepopt worden ist, wird wieder auf
S gepusht. uj wird
auf S gepusht.
Diagonalen von un zu allen Vertizes
auf S außer dem ersten und letzten ziehen.
2.0 Shading Problems
Es gibt Fälle, in welchen eine einfache Tesselierung
nicht zu einem akzeptablen Ergebnis führt.
Man muss dann bei der Tesselierung
einige Dinge berücksichtigen. Manchmal sind z.B. auf Polygonen Netze
aufgespannt (um Bowtie-Vierecke zu vermeiden). Dabei
stellt sich die Frage, welches der beste Weg ist, die durch das Netz
entstehenden Vierecke in Dreiecke zu zerlegen.
Es gibt verschiedene Ansätze, abhängig von gewünschten
Effekten:
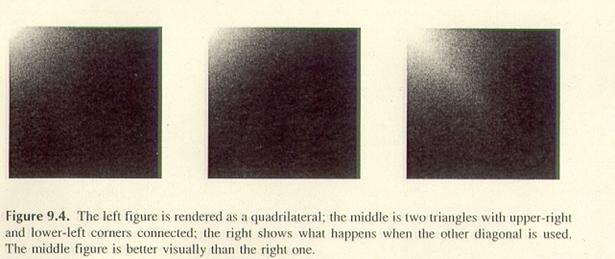
Für Vierecke ohne
zusätzliche Informationen ist es das Beste, die kürzere der beiden Diagonalen für
die Zerlegung zu verwenden.
Für Vierecke mit
unterschiedlichen Farbwerten pro Vertex ist es besser, die Vertices mit dem
kleinsten Farbwertunterschied zu verbinden.
Unten sieht man drei mal das gleiche Viereck. Das linke Bild zeigt das
ursprüngliche, das mittlere das korrekt tesselierte und
das rechte Bild das unakzeptabel tesselierte Viereck.
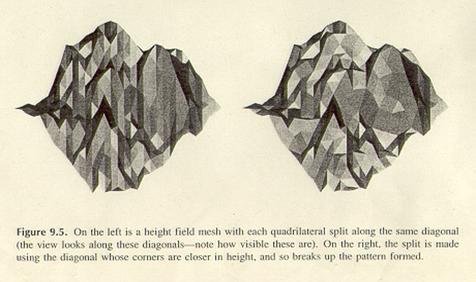
Auch bei
Landschaften kann es zu einem nicht akzeptablen Ergebnis bei der Tesselierung kommen. Hier gibt es mehrere Möglichkeiten,
dieses zu vermeiden. Zum Beispiel:
- diejenige
Diagonale zu nehmen, welche zwei gleich große Dreiecke produziert.
- Verbinden der
Vertices mit dem kleinsten oder größten Höhenunterschied. (Verfahren I)
Links ist immer die
gleiche Diagonale verwendet worden, rechts Verfahren I.
Es gibt Fälle, in
welchen Dreiecke das Innere von Vierecken nicht richtig darstellen können.
Ein Weg dieses zu
verbessern, ist ein Netz aufzuspannen, andere Texturinterpolationsschemata zu
wählen oder aber Gouard Shading auf das ganze
Viereck anzuwenden.
3.0 Edge Cracking
Einige Modelers benutzen NURBS (Non-Uniform
Rational B-Splines) um Kurven zu beschreiben
.
Über die
Splineflächen sind meistens Netze aufgespannt, um sie leichter rendern zu können.
Vorgehensweise:
Man geht
schrittweise über die Spline Kurve, definiert die
Fläche und berechnet den Vertex und die zugehörige
Diagonale.
Ein Problem kann
entstehen, wenn sich zwei Splineflächen treffen und die Punkte auf der
gemeinsamen Kante nicht für beide Flächen gleich sind. Das linke Bild zeigt wie
sogenannte Cracks entstehen können, wenn sich die Splineflächen treffen, das mittlere das korrigierte Bild
und das rechte das korrekte Bild ohne der Entstehung
von Cracks.
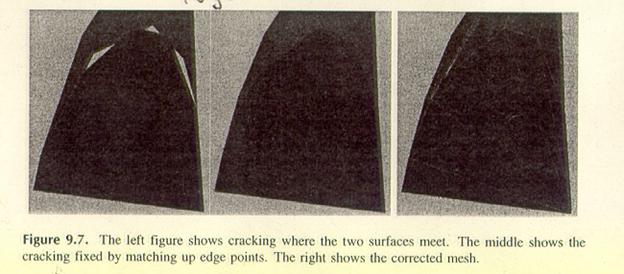
Edge Stitching nennt man den Prozess um dieses Problem zu
korrigieren. Dabei muss man sicherstellen, dass alle Punkte für beide
Splineflächen gleich sind.
4.0 T-Vertices
Dieses Problem entsteht, wenn zwei benachbarte Flächen versuchen,
die Vertizes an der gemeinsamen Kante zu teilen. Die
benachbarten Flächen können verschiedene Vertizes an
der gemeinsamen Kante haben. Dabei entsteht eine so genannte T- intersection .
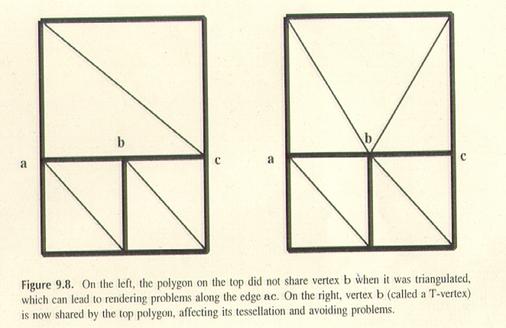
Dieses Problem kann total eliminiert werden, wenn man solche
Kanten sucht (meistens eine sehr schwierige Prozedur) und sicherstellt, dass
die Vertizes von allen angrenzenden Flächen geteilt
werden.
Wie man eine
T-intersection vermeiden kann, ist gut beschrieben im
Artikel von Cignoni, P., C. Montani, and R. Scopigno, "Triangulating Convex Polygons Having T-Vertices," journal
of graphics tools, vol.
1, no. 2, pp. 1-4, 1996.
Literature:
1. Real-Time Rendering, by Tomas Akenine-Möller and Eric Haines, ~880
pages, from A.K. Peters Ltd., 2nd edition
2. Computational geometry : algorithms and
applications / Mark de Berg; Marc van Krefeld….-2nd, rev.ed
Websites: www.opengl.org, flipcode.com, fly.srk.fer.hr, www.fh-landshut.de