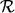 mit einer Ausprägung R.
Eine funktionale Abhängigkeit (engl. functional dependency) stellt
eine Bedingung an die möglichen gültigen Ausprägungen des Datenbankschemas
dar. Eine funktionale Abhängigkeit, oft abgekürzt als FD, wird dargestellt als
mit einer Ausprägung R.
Eine funktionale Abhängigkeit (engl. functional dependency) stellt
eine Bedingung an die möglichen gültigen Ausprägungen des Datenbankschemas
dar. Eine funktionale Abhängigkeit, oft abgekürzt als FD, wird dargestellt als
Gegeben sei ein Relationenschema
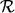 mit einer Ausprägung R.
Eine funktionale Abhängigkeit (engl. functional dependency) stellt
eine Bedingung an die möglichen gültigen Ausprägungen des Datenbankschemas
dar. Eine funktionale Abhängigkeit, oft abgekürzt als FD, wird dargestellt als
mit einer Ausprägung R.
Eine funktionale Abhängigkeit (engl. functional dependency) stellt
eine Bedingung an die möglichen gültigen Ausprägungen des Datenbankschemas
dar. Eine funktionale Abhängigkeit, oft abgekürzt als FD, wird dargestellt als
D. h., wenn zwei Tupel gleiche Werte für alle Attribute in ![]() haben, dann
müssen auch ihre
haben, dann
müssen auch ihre ![]() -Werte übereinstimmen. Anders ausgedrückt: Die
-Werte übereinstimmen. Anders ausgedrückt: Die
![]() -Werte bestimmen eindeutig die
-Werte bestimmen eindeutig die ![]() -Werte; die
-Werte; die ![]() -Werte sind
funktional abhängig von den
-Werte sind
funktional abhängig von den ![]() -Werten.
-Werten.
Die nächste Tabelle zeigt ein
Relationenschema ![]() über der Attributmenge
{ A, B, C, D}.
über der Attributmenge
{ A, B, C, D}.
| R | |||
| A | B | C | D |
| a4 | b2 | c4 | d3 |
| a1 | b1 | c1 | d1 |
| a1 | b1 | c1 | d2 |
| a2 | b2 | c3 | d2 |
| a3 | b2 | c4 | d3 |
Aus der momentanen Ausprägung lassen sich z. B. die funktionalen
Abhängigkeiten
{A} ![]() {B},{A}
{B},{A} ![]() {C},{C, D}
{C},{C, D} ![]() {B}
erkennen, hingegen gilt nicht
{B}
{B}
erkennen, hingegen gilt nicht
{B} ![]() {C}.
{C}.
Ob diese Abhängigkeiten vom Designer der Relation als semantische
Konsistenzbedingung verlangt wurden, läßt sich durch Inspektion der Tabelle
allerdings nicht feststellen.
Statt
{C, D} ![]() {B} schreiben wir auch
CD
{B} schreiben wir auch
CD ![]() B.
Statt
B.
Statt
![]()
![]()
![]() schreiben wir auch
schreiben wir auch
![]()
![]() .
.
Ein einfacher Algorithmus zum Überprüfen einer (vermuteten) funktionalen
Abhängigkeit
![]()
![]()
![]() in der Relation R lautet:
in der Relation R lautet: